Correct Answer

verified
Correct Answer
verified
Multiple Choice
TABLE 15-4
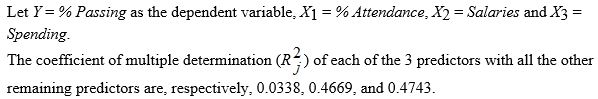 The output from the best-subset regressions is given below:
The output from the best-subset regressions is given below:
 Following is the residual plot for % Attendance:
Following is the residual plot for % Attendance:
 Following is the output of several multiple regression models:
Model (I) :
Following is the output of several multiple regression models:
Model (I) :
 Model (II) :
Model (II) :
 Model (III) :
Model (III) :
 -Referring to Table 15-4, the "best" model chosen using the adjusted R-square statistic is
-Referring to Table 15-4, the "best" model chosen using the adjusted R-square statistic is
A) X₁,X₃.
B) X₁,X₂,X₃.
C) Either of the above
D) None of the above
F) A) and C)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Which of the following will not change a nonlinear model into a linear model?
A) Quadratic regression model
B) Logarithmic transformation
C) Square-root transformation
D) Variance inflationary factor
F) A) and C)
Correct Answer

verified
Correct Answer
verified
True/False
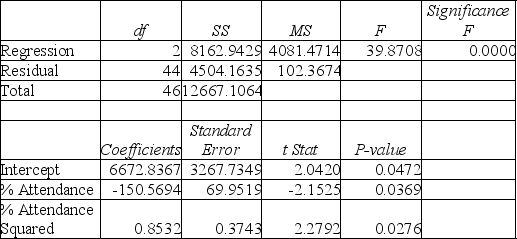
TABLE 15-3
A chemist employed by a pharmaceutical firm has developed a muscle relaxant. She took a sample of 14 people suffering from extreme muscle constriction. She gave each a vial containing a dose (X) of the drug and recorded the time to relief (Y) measured in seconds for each. She fit a "centered" curvilinear model to this data. The results obtained by Microsoft Excel follow, where the dose (X) given has been "centered."
 -Referring to Table 15-3, suppose the chemist decides to use an F test to determine if there is a significant curvilinear relationship between time and dose. If she chooses to use a level of significance of 0.01 she would decide that there is a significant curvilinear relationship.
-Referring to Table 15-3, suppose the chemist decides to use an F test to determine if there is a significant curvilinear relationship between time and dose. If she chooses to use a level of significance of 0.01 she would decide that there is a significant curvilinear relationship.
B) False
Correct Answer

verified
False
Correct Answer
verified
Multiple Choice
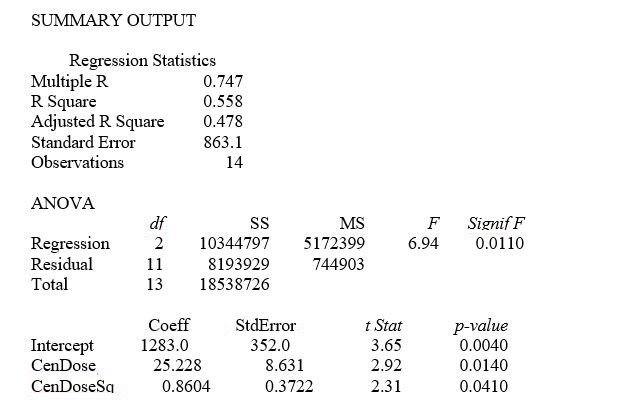
TABLE 15-1
A certain type of rare gem serves as a status symbol for many of its owners. In theory, for low prices, the demand increases and it decreases as the price of the gem increases. However, experts hypothesize that when the gem is valued at very high prices, the demand increases with price due to the status owners believe they gain in obtaining the gem. Thus, the model proposed to best explain the demand for the gem by its price is the quadratic model:
Y = β₀ + β₁X + β₁X² + ε
where Y = demand (in thousands) and X = retail price per carat.
This model was fit to data collected for a sample of 12 rare gems of this type. A portion of the computer analysis obtained from Microsoft Excel is shown below:  -Referring to Table 15-1, does there appear to be significant upward curvature in the response curve relating the demand (Y) and the price (X) at 10% level of significance?
-Referring to Table 15-1, does there appear to be significant upward curvature in the response curve relating the demand (Y) and the price (X) at 10% level of significance?
A) Yes, since the p-value for the test is less than 0.10.
B) No, since the value of β is near 0.
C) No, since the p-value for the test is greater than 0.10.
D) Yes, since the value of β is positive.
F) B) and C)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Which of the following is used to find a "best" model?
A) Odds ratio
B) Mallow's Cp
C) Standard error of the estimate
D) SST
F) A) and C)
Correct Answer

verified
Correct Answer
verified
True/False
The goals of model building are to find a good model with the fewest independent variables that is easier to interpret and has lower probability of collinearity.
B) False
Correct Answer

verified
Correct Answer
verified
True/False
Two simple regression models were used to predict a single dependent variable. Both models were highly significant, but when the two independent variables were placed in the same multiple regression model for the dependent variable, R² did not increase substantially and the parameter estimates for the model were not significantly different from 0. This is probably an example of collinearity.
B) False
Correct Answer

verified
Correct Answer
verified
True/False
TABLE 15-6
Given below are results from the regression analysis on 40 observations where the dependent variable is the number of weeks a worker is unemployed due to a layoff (Y) and the independent variables are the age of the worker (X₁), the number of years of education received (X₂), the number of years at the previous job (X₃), a dummy variable for marital status (X₄: 1 = married, 0 = otherwise), a dummy variable for head of household (X₅: 1 = yes, 0 = no) and a dummy variable for management position (X₆: 1 = yes, 0 = no).
The coefficient of multiple determination (R) for the regression model using each of the 6 variables Xⱼ as the dependent variable and all other X variables as independent variables are, respectively, 0.2628, 0.1240, 0.2404, 0.3510, 0.3342 and 0.0993.
The partial results from best-subset regression are given below:
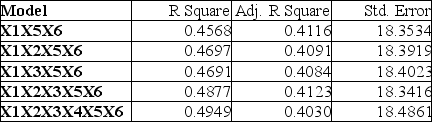 -Referring to Table 15-6, the model that includes all six independent variables should be selected using the adjusted r² statistic.
-Referring to Table 15-6, the model that includes all six independent variables should be selected using the adjusted r² statistic.
B) False
Correct Answer

verified
Correct Answer
verified
Short Answer
TABLE 15-6
Given below are results from the regression analysis on 40 observations where the dependent variable is the number of weeks a worker is unemployed due to a layoff (Y) and the independent variables are the age of the worker (X₁), the number of years of education received (X₂), the number of years at the previous job (X₃), a dummy variable for marital status (X₄: 1 = married, 0 = otherwise), a dummy variable for head of household (X₅: 1 = yes, 0 = no) and a dummy variable for management position (X₆: 1 = yes, 0 = no).
The coefficient of multiple determination (R) for the regression model using each of the 6 variables Xⱼ as the dependent variable and all other X variables as independent variables are, respectively, 0.2628, 0.1240, 0.2404, 0.3510, 0.3342 and 0.0993.
The partial results from best-subset regression are given below:
 -Referring to Table 15-6, what is the value of the variance inflationary factor of Age?
-Referring to Table 15-6, what is the value of the variance inflationary factor of Age?
Correct Answer

verified
Correct Answer
verified
Multiple Choice
If independent variables are not significant individually but are significant as a group at a specified level of significance, this is most likely due to
A) autocorrelation.
B) the presence of dummy variables.
C) the absence of dummy variables.
D) collinearity.
F) B) and C)
Correct Answer

verified
D
Correct Answer
verified
True/False
TABLE 15-6
Given below are results from the regression analysis on 40 observations where the dependent variable is the number of weeks a worker is unemployed due to a layoff (Y) and the independent variables are the age of the worker (X₁), the number of years of education received (X₂), the number of years at the previous job (X₃), a dummy variable for marital status (X₄: 1 = married, 0 = otherwise), a dummy variable for head of household (X₅: 1 = yes, 0 = no) and a dummy variable for management position (X₆: 1 = yes, 0 = no).
The coefficient of multiple determination (R) for the regression model using each of the 6 variables Xⱼ as the dependent variable and all other X variables as independent variables are, respectively, 0.2628, 0.1240, 0.2404, 0.3510, 0.3342 and 0.0993.
The partial results from best-subset regression are given below:
 -Referring to Table 15-6, the variable X₄ should be dropped to remove collinearity.
-Referring to Table 15-6, the variable X₄ should be dropped to remove collinearity.
B) False
Correct Answer

verified
Correct Answer
verified
True/False
So that we can fit curves as well as lines by regression, we often use mathematical manipulations for converting one variable into a different form. These manipulations are called dummy variables.
B) False
Correct Answer

verified
Correct Answer
verified
True/False
The stepwise regression approach takes into consideration all possible models.
B) False
Correct Answer

verified
Correct Answer
verified
Short Answer
TABLE 15-4
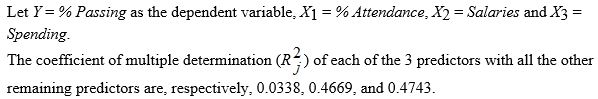 The output from the best-subset regressions is given below:
The output from the best-subset regressions is given below:
 Following is the residual plot for % Attendance:
Following is the residual plot for % Attendance:
 Following is the output of several multiple regression models:
Model (I):
Following is the output of several multiple regression models:
Model (I):
 Model (II):
Model (II):
 Model (III):
Model (III):
 -Referring to Table 15-4, what is the p-value of the test statistic to determine whether the quadratic effect of daily average of the percentage of students attending class on percentage of students passing the proficiency test is significant at a 5% level of significance?
-Referring to Table 15-4, what is the p-value of the test statistic to determine whether the quadratic effect of daily average of the percentage of students attending class on percentage of students passing the proficiency test is significant at a 5% level of significance?
Correct Answer

verified
0.0276
Correct Answer
verified
Multiple Choice
As a project for his business statistics class, a student examined the factors that determined parking meter rates throughout the campus area. Data were collected for the price per hour of parking, blocks to the quadrangle, and one of the three jurisdictions: on campus, in downtown and off campus, or outside of downtown and off campus. The population regression model hypothesized is Yᵢ = β₀ + β₁X₁ᵢ + β₂X₂ᵢ + β₃X₃ᵢ + ε where Y is the meter price X₁ is the number of blocks to the quad X₂ is a dummy variable that takes the value 1 if the meter is located in downtown and off campus and the value 0 otherwise X₃ is a dummy variable that takes the value 1 if the meter is located outside of downtown and off campus, and the value 0 otherwise Suppose that whether the meter is located on campus is an important explanatory factor. Why should the variable that depicts this attribute not be included in the model?
A) Its inclusion will introduce autocorrelation.
B) Its inclusion will introduce collinearity.
C) Its inclusion will inflate the standard errors of the estimated coefficients.
D) Both B and C.
F) A) and C)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
TABLE 15-1
A certain type of rare gem serves as a status symbol for many of its owners. In theory, for low prices, the demand increases and it decreases as the price of the gem increases. However, experts hypothesize that when the gem is valued at very high prices, the demand increases with price due to the status owners believe they gain in obtaining the gem. Thus, the model proposed to best explain the demand for the gem by its price is the quadratic model:
Y = β₀ + β₁X + β₁X² + ε
where Y = demand (in thousands) and X = retail price per carat.
This model was fit to data collected for a sample of 12 rare gems of this type. A portion of the computer analysis obtained from Microsoft Excel is shown below:  -Referring to Table 15-1, what is the correct interpretation of the coefficient of multiple determination?
-Referring to Table 15-1, what is the correct interpretation of the coefficient of multiple determination?
A) 98.8% of the total variation in demand can be explained by the linear relationship between demand and price.
B) 98.8% of the total variation in demand can be explained by the quadratic relationship between demand and price.
C) 98.8% of the total variation in demand can be explained by the addition of the square term in price.
D) 98.8% of the total variation in demand can be explained by just the square term in price.
F) A) and B)
Correct Answer

verified
Correct Answer
verified
True/False
TABLE 15-6
Given below are results from the regression analysis on 40 observations where the dependent variable is the number of weeks a worker is unemployed due to a layoff (Y) and the independent variables are the age of the worker (X₁), the number of years of education received (X₂), the number of years at the previous job (X₃), a dummy variable for marital status (X₄: 1 = married, 0 = otherwise), a dummy variable for head of household (X₅: 1 = yes, 0 = no) and a dummy variable for management position (X₆: 1 = yes, 0 = no).
The coefficient of multiple determination (R) for the regression model using each of the 6 variables Xⱼ as the dependent variable and all other X variables as independent variables are, respectively, 0.2628, 0.1240, 0.2404, 0.3510, 0.3342 and 0.0993.
The partial results from best-subset regression are given below:
 -Referring to Table 15-6, the model that includes X₁, X₂, X₃, X₅ and X₆ should be among the appropriate models using the Mallow's Cp statistic.
-Referring to Table 15-6, the model that includes X₁, X₂, X₃, X₅ and X₆ should be among the appropriate models using the Mallow's Cp statistic.
B) False
Correct Answer

verified
Correct Answer
verified
Short Answer
TABLE 15-4
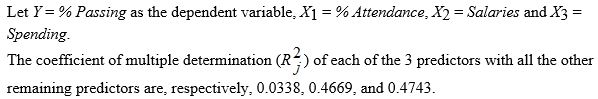 The output from the best-subset regressions is given below:
The output from the best-subset regressions is given below:
 Following is the residual plot for % Attendance:
Following is the residual plot for % Attendance:
 Following is the output of several multiple regression models:
Model (I):
Following is the output of several multiple regression models:
Model (I):
 Model (II):
Model (II):
 Model (III):
Model (III):
 -Referring to Table 15-4, what is the value of the test statistic to determine whether the quadratic effect of daily average of the percentage of students attending class on percentage of students passing the proficiency test is significant at a 5% level of significance?
-Referring to Table 15-4, what is the value of the test statistic to determine whether the quadratic effect of daily average of the percentage of students attending class on percentage of students passing the proficiency test is significant at a 5% level of significance?
Correct Answer

verified
Correct Answer
verified
True/False
TABLE 15-3
A chemist employed by a pharmaceutical firm has developed a muscle relaxant. She took a sample of 14 people suffering from extreme muscle constriction. She gave each a vial containing a dose (X) of the drug and recorded the time to relief (Y) measured in seconds for each. She fit a "centered" curvilinear model to this data. The results obtained by Microsoft Excel follow, where the dose (X) given has been "centered."
 -Referring to Table 15-3, suppose the chemist decides to use an F test to determine if there is a significant curvilinear relationship between time and dose. If she chooses to use a level of significance of 0.05, she would decide that there is a significant curvilinear relationship.
-Referring to Table 15-3, suppose the chemist decides to use an F test to determine if there is a significant curvilinear relationship between time and dose. If she chooses to use a level of significance of 0.05, she would decide that there is a significant curvilinear relationship.
B) False
Correct Answer

verified
Correct Answer
verified
Showing 1 - 20 of 96
Related Exams